GeoSpirale

Information: 

Vom Rondell der 

Plassenburg. 

habt ihr einen wunderbaren Blick auf Kulmbach und das Umland. Mit besonders guten Adleraugen könnt ihr vielleicht auch den Cache sehen. Ein Besuch lohnt sich auf jeden Fall. 

Aufgabe: 

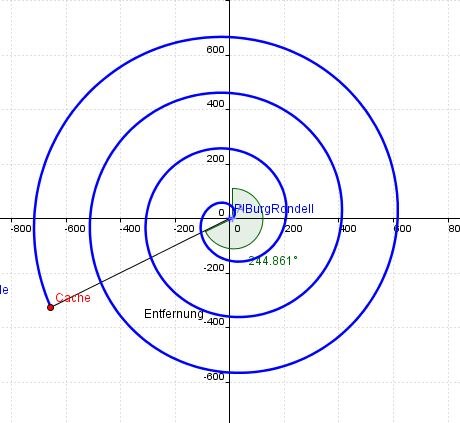
1. Von diesem Startpunkt (32 U 676075 5553543) wandert gegen den Uhrzeigersinn auf einer Spirale, die auf den griechischen Mathematiker Archimedes zurück geht. 

2. Die Form der Spirale berechnet/konstruiert mit folgenden Werten:
   a = 65,234  ("Windungsabstand")
   r(φ) = a * φ

3. φ ist der Winkel im Bogenmaß.
   r ist der "Radius" vom Nullpunkt zu irgendeinem Punkt auf der Spirale. Dieser entspricht damit der Entfernung des Caches vom Startpunkt aus.

4. Nachdem ihr eine Strecke von s = 4228,17 Meter auf dieser Spirale gewandert seid, findet ihr den Cache. 

Anmerkungen: 

• Ein sehr exaktes Arbeiten ist nötig.

• Bitte das Ganze als mathematische (Karten-)Konstruktion mit UTM betrachten, nichts mit Erdkrümmung, Kugeln, Wegpunktprojektion, usw. rechnen. Es reichen normale trigonometrische und geometrische Grundkenntnisse aus. Die Konstruktion ist mit Millimeterpapier oder Karte mit Zirkel und Lineal durchzuführen. (D5) 

• Das für private Zwecke kostenlose Programm GeoGebra könnte eine perfekte Hilfe sein. GeoGebra kann online im Browser ausgeführt werden. Es muss weder heruntergeladen noch auf dem Computer installiert werden. Eine Registrierung ist ebenfalls nicht notwendig. (D<5)

• Ich empfehle, nicht wirklich 4228,17 Meter weit auf der Spirale zu wandern. In diesem Fall wäre die Terrainwertung ebenfalls 5. Der Cache liegt vom Rondell aus in weniger als 1km Entfernung. Eine Parkmöglichkeit erhaltet ihr bei richtiger Lösung mit dem Geochecker. Vom Parkplatz zum Cache sind es dann ca. 200m zum Döschen. 

• Die Beispiel-Konstruktion ist weder maßstäblich noch in der richtigen Lage. 

• Die Lösung kann hier überprüft werden.  

Viel Spaß beim rechnen, konstruieren und suchen!
Siegfried, dl8nab

Weitere dl8nab-Caches findest du hier -->