Página de inicio
Artículo publicado en
CQ Radio Amateur, nº 241 (enero 2004)
Ondas de radio y antenas: una explicación
práctica
Se describe de manera llana pero completa
principios básicos de radiación y de antenas, del máximo
interés de cualquier radioaficionado
Sergio Manrique Almeida
Todos los derechos reservados

Introducción
Un transmisor de radio no hace más que generar
una señal eléctrica, una energía que al llegar a la antena se
transforma en una onda de radio que es enviada al espacio.
Una onda de radio es una onda electromagnética,
es decir, la suma de un campo eléctrico y un campo magnético que
varían con el tiempo de acuerdo con una misma frecuencia.
Al variar con el tiempo es como esos campos
propagan la energía por el espacio; esa energía, al llegar a
la antena receptora se vuelve a convertir en una señal eléctrica
que va a nuestros receptores.
No puede existir un campo eléctrico variable
con el tiempo sin otro campo magnético variable con el tiempo, y
viceversa.
Campo próximo y campo lejano
El campo electromagnético generado por una
antena se divide además en:
- Campos próximos, también denominados campos
inducidos. Son los que predominan en las cercanías de la antena, a
distancias mucho menores que 0,16 longitudes de onda. Decrecen con
el cuadrado de la distancia.
- Campos lejanos, también llamados campos radiados.
Predominan a distancias de la antena mayores de una longitud de
onda, y son los que permiten las comunicaciones por radio.
Decrecen con la distancia, es decir:
E = H = E0, H0 son
constantes; "d" es la distancia.
La energía propagada por un campo
electromagnético en el vacío o la atmósfera viene dada por E · H =
E2 / 377 = E02 / 377d2
En efecto, como veremos más adelante, la
potencia emitida decrece con el cuadrado de la distancia. (Nota:
377 es la impedancia característica del medio, en este caso el
vacío).
Ondas planas, polarización
A distancias de la antena superiores a varias
longitudes de onda, se puede considerar que las líneas de campo
(que será solamente campo radiado) localmente son rectas, y por
ello son denominadas ondas planas. Son las que en la práctica
permiten las comunicaciones. Las vemos en las figuras 1 y 2, para
polarizaciones vertical y horizontal respectivamente. La
polarización de una onda plana viene dada por la orientación de su
componente de campo eléctrico, que a su vez se corresponde con la
orientación de la antena si físicamente es recta (dipolos, Yagis,
verticales, hilos largos, etc.).
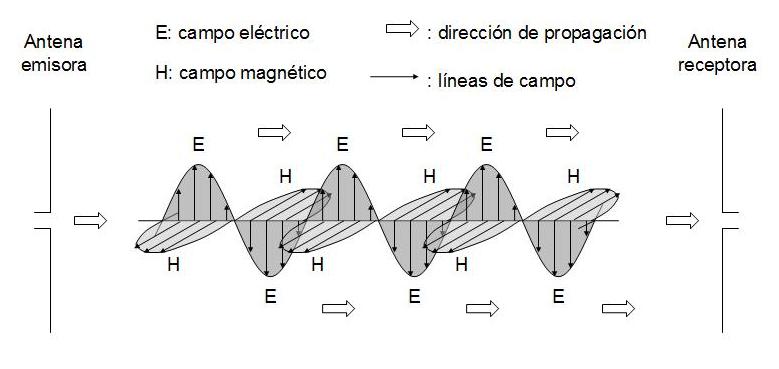
Figura 1. "Fotograma" de una onda de radio plana de
polarización vertical, para un instante dado. En la realidad, la
onda se iría desplazando hacia la derecha.
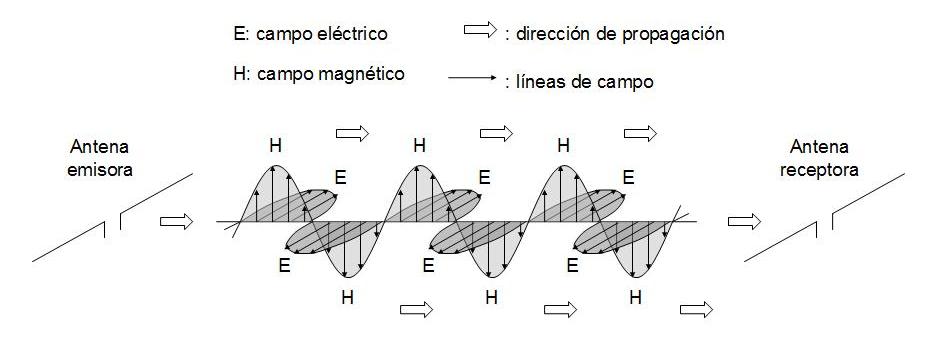
Figura 2. Lo mismo que en la figura 1 pero en polarización
horizontal.
Como se observa en las figuras 1 y 2, las líneas de campo
eléctrico (E) y magnético (H), representadas por las "flechas",
son perpendiculares. La amplitud de cada "flecha" nos da la
intensidad de campo (E ó H) en cada punto en un instante dado;
dicha intensidad varía de acuerdo con la frecuencia de la onda
de radio, va cambiando entre las crestas superior e inferior; es
lo mismo que si el lector imaginase las ondas de ambas figuras
desplazándose hacia la derecha.
Las líneas de campo solamente existen sobre
el papel: están relacionadas con la única descripción posible de
las ondas de radio, es decir, la descripción mediante el
lenguaje matemático. En este artículo no se seguirá ese camino,
solamente decir que el trazado y los valores de las líneas de
campo se obtienen a partir de la resolución de las ecuaciones de
Maxwell, que gobiernan todo fenómeno electromagnético.
Campos e
impedancia de una antena
Toda antena presenta en sus bornes una
impedancia Za = Ra + jXa. Las
antenas comerciales para radioaficionado habitualmente son
construidas para presentar una impedancia Za cercana
a 50 +j0 ohmios (en su frecuencia de resonancia), para poder ser
conectadas directamente a nuestros transceptores mediante líneas
coaxiales de 50 ohmios.
Ra es la resistencia de radiación, y está
asociada a los campos radiados, también llamados lejanos.
Xa es la componente no resistiva de la
impedancia de la antena, y está asociada a los campos
inductivos, también llamados cercanos.
Densidad de potencia radiada
Supongamos un transmisor de 10 watios en la
banda de 144 MHz, que corresponde a una longitud de onda de 3·108
/ 144·106 =
aproximadamente 2 metros (3·108 es la velocidad de la
luz en el vacío, en metros/segundo).
El transmisor está conectado a una antena
isotrópica, es decir, una antena que radia la misma energía en
todas las direcciones; una vertical de 1/4 de longitud de onda
con 3-4 radiales muy elevada sobre el suelo es casi isotrópica.
Supóngase además que se dan condiciones de espacio
libre: no hay objetos en el entorno de las antenas que
perturben la propagación, no hay onda reflejada en tierra o es
despreciable, y las antenas están bastante elevadas (en términos
de longitud de onda). Es decir, solamente hay una onda, que es
directa, entre las antenas. Estas condiciones de espacio libre
se darán más fácilmente con antenas de elevada directividad.
A una distancia "d" (en metros) de la antena
emisora, la densidad de potencia radiada, "P", vendrá dada por
P = W / 4·3,1416·d2 watios/metro
cuadrado (esta ecuación es válida solamente para distancias
mucho mayores que la longitud de onda).
A un kilómetro, tendremos P = 10 /
(4·3,1416·10002) = 0,8 microwatios por m2.
(Nota: 3,1416 es el número "pi").
La potencia emitida se reparte por igual en
todas direcciones (antena emisora isotrópica). Cuanto mayor es
la distancia de la antena emisora, menor es la densidad de
potencia, es decir, la potencia por metro cuadrado.
Potencia
recibida en espacio libre. Área efectiva de una antena
La antena receptora captará una parte de esa densidad de
potencia (figura 3), ya que se comporta como una "ventana"
(círculo sombreado en la figura) orientada de cara a la antena
emisora. Esa ventana, llamada área efectiva, tiene una
superficie de "A" m2.
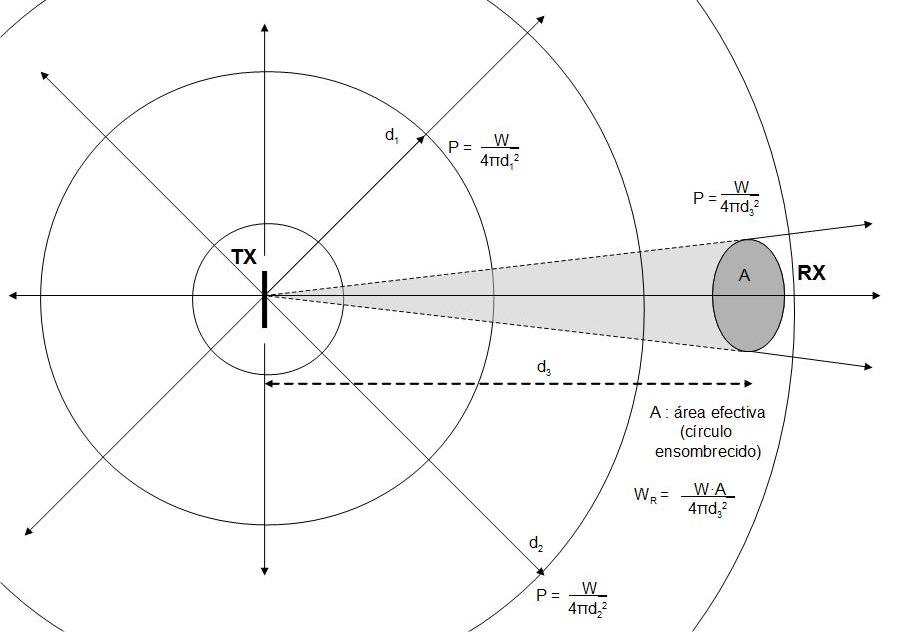
Figura 3. Ver
texto. Transmisor con antena isotrópica (radia de igual modo
en todas direcciones), y receptor con antena de área efectiva
A.
Así, la potencia
captada por la antena receptora será WR = W·A /
4·3,1416·d2 watios.
El área efectiva de una antena viene dada por A = L2·G
/ 4·3,1416
L: longitud de onda en metros.
3,1416: número "pi".
G: ganancia de la antena respecto isotrópico (respecto un
dipolo de media onda más 2,1 dB). Aquí no hay que poner la
ganancia en decibelios, sino en términos lineales: para una
antena con una ganancia de N dBi (dB respecto
isotrópico), el valor lineal de su ganancia en la ecuación
será G = 10 (N/10).
(Un inciso para los que ahora empiezan: la ganancia de una
antena se define como su capacidad de concentrar hacia una
dirección o direcciones de interés la radiación que emita, en
detrimento del resto de direcciones, actuando del mismo modo
en recepción).
-Una antena de L/4 (un cuarto de onda), como a la que nos
referíamos, para la banda de 144 MHz, tendrá una ganancia G =
100,03 = 1,07, y un área eficaz A = 0,32 m2.
-Una antena isotrópica tendrá G = 100 = 1.
-Un dipolo de media onda para la frecuencia de 3,7 MHz (banda
de 80 metros) tiene un área efectiva
A = 10 (0,21) · 802 / 4·3,1416 =
2595 m2.
-Un dipolo de media onda para 144 MHz tiene un área efectiva A
= 10 (0,21) · 22 / 4·3,1416 = 0,5 m2.
-Una formación de antenas para 144 MHz con una ganancia de 16
dBi tendrá un área eficaz A = 10 m2.
Las mencionadas antenas para 144 MHz, a un
kilómetro del emisor captarán una potencia de:
-Antena de L/4 elevada, WR = 0,8·10-6
watios/m2 · 0,32 m2 = 0,26 microwatios
-Dipolo, WR = 0,8·10-6 watios/m2
· 0,5 m2 = 0,4 microwatios
-Formación de antenas, WR = 0,8·10-6
watios/m2 · 10 m2 = 8 microwatios.
Aparte de condiciones de espacio libre, en
todo lo anterior hemos supuesto además que todas las antenas
tienen la misma polarización, y que el medio de propagación
(la atmósfera) no introduce pérdidas.
Hemos introducido el concepto de área
efectiva de una antena ya que a muchos lectores les dará una
nueva perspectiva de las antenas. El área efectiva no coincide
necesariamente con el área geométrica de la antena.
Longitud efectiva de una antena
Es un parámetro también utilizado para
definir antenas que físicamente son lineales.
Vca = E·Lef
Vca es el voltaje creado en los bornes de la antena
(en circuito abierto), sometida a un campo electromagnético
que tiene una intensidad de campo eléctrico de E
voltios/metro. La longitud efectiva es la relación entre los
valores de ambos. Se supone que el campo electromagnético y la
antena tienen la misma polarización.
La longitud efectiva también puede
definirse como la relación entre la corriente creada en la
antena (con sus bornes en cortocircuito) y la intensidad de
campo magnético (H amperios/metro) del campo al que está
sometida:
Icc = H·LefH
La longitud efectiva puede calcularse a
partir del área efectiva, y no tiene por qué coincidir con la
longitud física de la antena. Naturalmente, tanto la longitud
eficaz como el área efectiva de una antena se calculan en la
dirección de máxima ganancia.
Atenuación con la
distancia… y la frecuencia
Pero en la práctica de los radioaficionados,
al hablar de la ganancia de una antena siempre lo hacemos en
términos de dB, sean dBi (respecto isotrópico) o dBd (respecto
dipolo). Así, ¿cómo obtener WR, la potencia recibida
en función de las ganancias de las antenas? Bien, ahora ya
consideremos que la antena emisora no es isotrópica, tiene una
cierta ganancia GT.
WR = WT·A·GT
/ 4·3,1416·d2 = (WT·A / 4·3,1416·d2)
· (L2·GR / 4·3,1416)· GT
= WT · GT · GR · (L /
4·3,1416·d)2
GT, GR: ganancias (lineales, no en dBi) de
la antena transmisora y de la receptora.
WT, WR: potencias transmitida y recibida,
en watios.
La ecuación es válida para "d" mucho mayor que la longitud de
onda (L). Traducida a decibelios, será:
WR (dBW) = WT (dBW) + GT (dBi)
+ GR (dBi) + 20 log (L) - 20 log (4·3,1416·d)
WT/R (dBW) = 10 log (WT/R), potencias en
dBW (decibelios respecto un watio).
log: logaritmo base 10.
Supongamos el QSO entre las dos estaciones de la figura
4. Seguimos considerando condiciones de espacio libre y que la
atmósfera no introduce pérdidas.
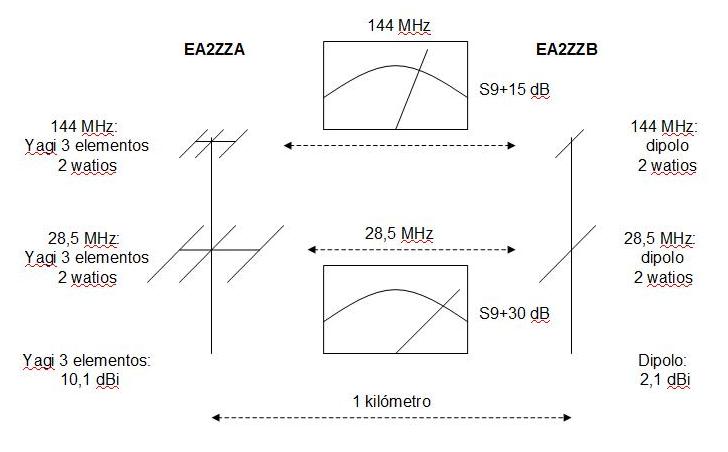
Figura 4. Ver
texto. En la figura se supone que los "S-meter" se comportan
por igual en HF y en VHF.
La potencia recibida en
28,5 MHz en bornes de antena de cada estación será:
2·10 (10,1/10)·10 (2,1/10) · (10,5 /
4·3,1416·1000) = 23 microwatios.
Ambas estaciones reciben la misma señal porque emplean la
misma potencia (otra cosa será que el "S-meter" de una de las
dos sea más "tacaño" que el de la otra, no sería de extrañar).
Si pasan a 144 MHz, también con una Yagi de 3 elementos, un
dipolo, y 2 watios, la potencia recibida en antena por ambas
será:
2·10 (10,1/10)10 (2,1/10) · (10,5 /
4·3,1416·1000) = 0,8 microwatios.
Éste es un punto que sorprenderá a muchos.
Las antenas son equivalentes, pero al pasar de 28,5 MHz a 144
las señales bajan 14 dB, más de dos unidades "S" en los
"S-meter" respectivos.
En resumidas cuentas: un watio en 28,5 MHz
equivale a 29 watios en 144 MHz; y un watio en 144 MHz
equivale a 9 watios en 432 MHz. A mayor frecuencia, menores
señales para iguales potencia, distancia y antenas
equivalentes. De todas maneras es un consuelo pensar que a
mayor frecuencia (menor longitud de onda) también es más fácil
construir antenas de ganancia elevada, y el ruido atmosférico
es menor.
Diagrama de radiación y distancia
El diagrama de radiación de una antena es la expresión
gráfica del modo en que una antena emite o recibe mayores o
menores señales según la dirección; en la figura 5 vemos un
ejemplo de diagrama de radiación. Si se quiere obtener
experimentalmente el diagrama de radiación de una antena, las
medidas de campo deben hacerse a una distancia mínima de
varias longitudes de onda, ya que en las cercanías de la
antena el diagrama es muy diferente, está distorsionado, y no
será el que capten nuestros corresponsales en la distancia.
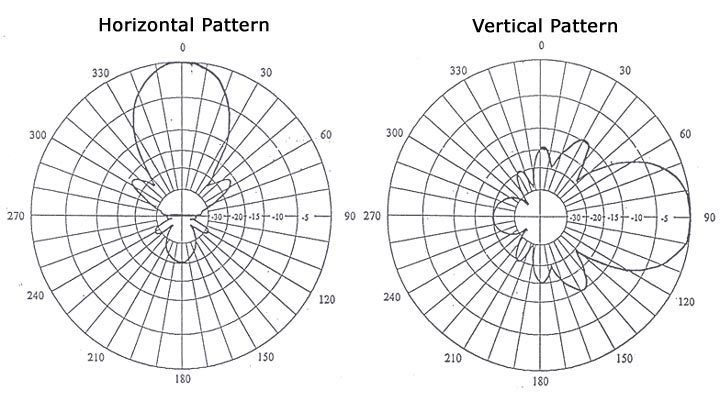
Figura 5. Ejemplo
de diagramas de radiación en el plano horizontal y en el
vertical; corresponden a una antena Yagi comercial para la
banda de 2,4 GHz (fuente: YDI Wireless).
Bibliografía
A. Cardama, "Notas de antenas", ETSETB, Universidad
Politécnica de Cataluña, 1992.
Página
de inicio




