|
|
  
Parabola per 2,4 Ghz
|
Parabola per 2.4 Ghz
Seconda sperimentazione
Cerchietti per 2.4 Ghz su una parabola a primo fuoco da un 1 metro circolare, acquistata in fiera per realizzare il mio primo sogno di ricevere i 2.4 Ghz, su una parabola di grandi dimensione per poter ricevere è fare dei contest con un buon guadagno di 24bD, le prove sono state fatte sul mio balcone per cui ho la direzione del ponte del
BEACON 2.4Ghz. Nella mia zona dove abito, dei radioamatori hanno realizzato un
beacon per 2.4 Ghz, con un
Convertitore in banda 1.2 / 2.4 Ghz, con una parabola offset con i
Cerchietti ho avuto grande successo nel ricevere il
beacon 2.4Ghz. |

click |
|
 click
click |
Cerchietti al centro alla Parabola
La ricezione del primo tentativo
Cerchietti 2,4
in parabola offset, ho utilizzato anche questo tipo di soluzion e, con una parabola da 100 cm, quella usata per
meteo sat foto sopra, le misure per i cerchietti sono reali del mio primo prototipo,
solo il vantaggio di poter utilizzare al centro, i cerchietti per poter conoscere la distanza e
il rapporto del diametro di una parabola per il suo fuoco potrete
ricavare il rapporto D/F (Diametro/Focale) dobbiamo sapere prima
la sua profondità della (BOMBATURA) della parabola, utilizziamo una riga depositiamo fra le due estremità del
bordo della parabola è misuriamo al centro, supponiamo che avete al centro la misura di 13,5 cm
, come il mio caso. |
|
Parabola 100 cm
Conoscendo il diametro della parabola potremmo calcolare il
fuoco sarà anche quello che ci permetterà di determinare il valore di
( P ) Profondità ,
dal mio caso
13,5 cm, perciò il calcolo avviene ricavata con la seguente formala :
y=4 D x (f/D)
dove :
- D è il diametro della parabola
- f il fuoco
- x,y coordinate del punto P generico
Formula P = D x D : (
C x F16 )
Parabola da 100
Diametro D x D 100 X 100 =10.000
Profondità C13,5 x F16 = 216
Diametro 10.000 : 216 = (46,29629629) 46,3
IL rapporto la misurare fra al centro della parabola, al centro dei cerchietti,
vedi disegno, fattore di FUOCO la lunghezza e pari di 46,3 cm esatti.
IL valore non possiamo arrotondare a 46 cm,
perché
la profondità della parabola influisce sul guadagno e anche il rumore,
rimane che il rapporto D/F dentro il limite da noi indicato cioè 46,3 cm, otteniamo sempre alto
rendimento e bassa cifra di rumore.
Questa formula può risultare utile quando si ha
disposizione una parabola, e non conosciamo la profondità e il fuoco, nota che il
Diametro D, la Profondità C, Fuoco F le misure sono
state fatte in centimetri. |

NEL FUOCO (chiamato anche PUNTO
FOCALE).
Ecco come si calcola il punto
focale di una parabola: Punto focale = (D * D ) / (16 * P) D
= diametro parabola P = profondità della parabola in cm
 click
click |
| |
|
Parabola
|
DB
|
DB
|
|
Diametro in metri |
Guadagno parziale
minimo |
Guadagno
parziale massimo |
|
1,00 |
38,5dB |
40.2dB |
|
1,20 |
40,0dB |
41,8dB |
|
1,40 |
41,4dB |
43,1dB |
|
1,50 |
42,0dB |
43,7dB |
|
1,60 |
42,5dB |
44,3dB |
|
1,70 |
43,1dB |
44,8dB |
|
1,80 |
43,5dB |
45,3dB |
|
1,90 |
44,0dB |
45,8dB |
|
2,00 |
44,5dB |
46,2dB |
|
2,20 |
45,3dB |
47,1dB |
|
2,40 |
46,5dB |
47,8dB |
|
2,50 |
46,5dB |
48,1dB |
|
|
Tabella (1)
Guadagno
click |
Guadagno di una parabola
Il Guadagno in potenza di una parabola in teoria si ricava con la seguente formula:
G = Pi x (D x Mhz : 300) x n
G=Guadagno
Pi= pi-grego 3,14
D= Diametro della parabola
Mgz= Frequenza di Ricezione
n= Rendimento
La frequenza di ricezione sulla banda 2,445 Mgz per calcolare il guadagno si considera la frequenza pari a Ghz 2,445 x 100 = 244,500 : 300 = 815 x 815 = 664,225
Poiché conosciamo il valore di (Pi) al quadrato cioè 9,8596 possiamo eseguire con successo operazione:
Pi=3,14 x 3,14 = 9,8596 x 664,225
6,548999281x0.50=3,274496405 vedi tabella (1)
315x 315 = 9,8596 x 664,225
6,548999281 x 0.75 2,454955872
vedi tabella
(1)
G = minimo al numero 3,274 0,50 = db 35,1
G = massimo al numero 2,454 0,75 = dB 33,9
Da questa tabella potete ricavare il guadagno in potenza conoscendo il valore dei dB conoscendo il guadagno in potenza in rapporto al diametro ed alla frequenza di lavoro. |
|
 click click |
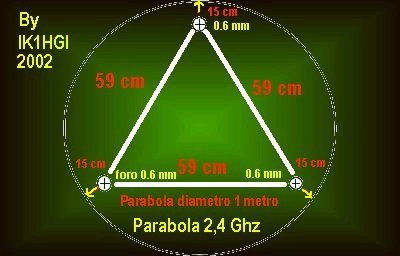
Misure da realizzare sulla parabola
Una volta stabilito le misure calcolate la distanza, da sistemare i cerchietti al centro. Ricavare 3 barre filettate del 0.6 mm, trovare il punto esatto, ho fatto in modo molto semplice con un metro misure 15 cm della bordo della parabola, verso al centro, la diagonale dei 3 punti la distanza fra un punto di angoli da una estremità la misura è 59 cm, fare in modo che sia un triangolo al centro della parabola, per trovare esattamente il punto esatto, tagliate un tondino di legno in misura di 59 cm, questo punto trovate un triangolo perfetto, appoggiare sulla parabola dove avete tranciato i 15 cm, il risultato sotto nella foto.
click
|
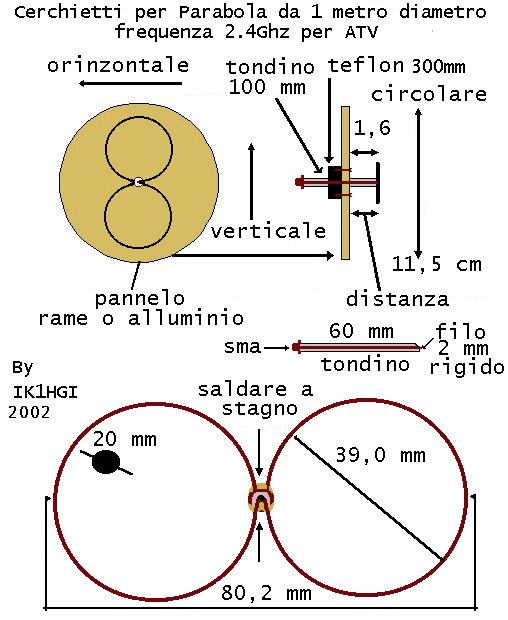
Schema blocchi del materiale
Riflettore alluminio circolare 11,5 spessore 0,1 mm
Barra filettata del 0,6 mm
Bocchettone " F "
Cerchietti spessore 0,2 del diametro 39,0 mm
Scatola di plastica tipo(Mascarpone devi foto)
Teflon del diametro 30x 25x10 cm
Tondino di rame del 10x60 ( la lunghezza non comporta nulla)
Filo interno del 0,2 mm
Lamierino tenuta riflettore 20x 6,5 cm
|
 click
click |
|
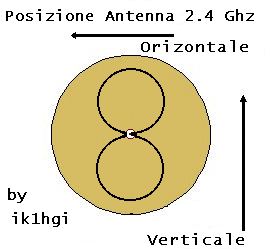 |
Disposizione riferimento
alla ricezione 2,4 Ghz
ORIZZONTALE - VERTICALE |
|
 click
click
Barattolo
Ottone |
Barattolo di ottone
Ho utilizzato 2 soluzioni, una con un barattolo di
alluminio da caffè, lo trovate sui bancarelle dei mercati, (Caffè & zucchero) oppure trovate un laminato di
ottone da 0,8 mm, con facilità di rotolare, per formare un barattolo come vedi la foto, le misure fra il barattolo di
alluminio
e quello di
ottone
hanno la stessa misura, solo cambia il tipo di materiale. |
|
 click click
Barattolo e Fascetta |
Componenti
La fascetta da utilizzare si può utilizzare qualsiasi materiale che possa tenere bene rigido in contenitore, le fascette che ho utilizzato sono del materiale in acciaio.
|
|
 click
click
Barattolo
Alluminio |
Barattolo di alluminio
Barattolo da caffé sulla parabola da 1 metro diametro, prove è sperimentazione ottenute per la ricezione sui 2,4 Ghz.
|
|
 click click
Barattolo in Disegno |
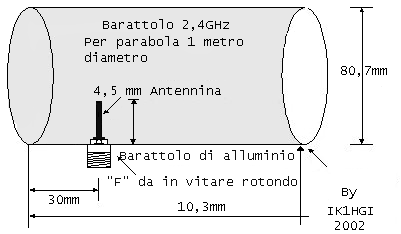
Barattolo di alluminio
Larghezza circolare 90,8 mm
Lunghezza profondità 130 mm
Spessore 0,1 o 0,8 mm
L'antenna 4,0 mm (rispettate anche il datino)
Bocchettone del tipo "F" altro medito per realizzare
l' antenna
a barattolo con vari formule.
|
|
 click
click
Parabola con barattolo |
Parabola con barattolo
Fra le caratteristiche barattolo e cerchietti cambia il modo come volete realizzare il tipo di lavoro, fate in modo con molta cautela e con certezza di rispettare i cm, mm, buon lavoro.
73 Antonio IK1HGI
|
|
|



 click
click

 click
click




 click
click click
click