A Small Study of Card Pyramids
By James PalmerUPDATE (5/14/2008)
I was able to offload the pictures taken on my cellular phone, and lo and behold a picture of the card pyramid was on it. If you examine it closely, there in fact six stories! Success!

INCOMPLETE.
Come one evening at Aggie Fish Camp a friend of mine and I were unoccupied in a lounge. There we found a deck of cards that was not up to game playing specification, so we chose to build card houses. At first we only tried our hands at the four-side box kind of houses, but after while we felt up to the challenge of a card pyramid.
Upon completion of the pyramid we had supposedly used all the cards in the mixed-up deck, and everyone who saw the pyramid took great delight in it. That was all fine and well until I got home. I was going to tell everybody how big it was, but I was at a loss to remember how many stories to tell Thus I had to reconstruction the bit of information from the knowledge of how many cards were used. (Ostensibly 47 were used.)
Knowing that card pyramids such as this are built using a very regular pattern, I figure it would be easiest to construct a sum of all cards in the pyramid based on the number of stories used. Stories, as used in this text, refers to the the number of vertical levels in the pyramid.
Starting from the apex of any pyramid we start with two cards. The apex is simply a "triangle" created by two cards on top. Similarly, the next level is the horizontal card supporting the apex and the four cards forming two "triangles". Likewise, the next level is the horizontal cards and all triangles supporting these horizontal cards. This simply goes on and on until you're at the surface supporting the pyramid.
For each "triangle" we have two cards, and for each level there is exactly one horizontal card less than the story number of that level, and there are as many "triangles" as the story number. The story number is simply what story the card is, starting with 1 being the apex.
So, for a single level (n) the number of cards in it will be:
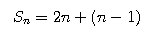
Now, taking this one step further we can simplify our sum:
S = 3n - 1
Now, we can write out the sum of the entire pyramid as a sum of each story (for k stories in a pyramid):
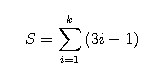
Armed with this information we are capable of solving for how many stories our pyramid has.
Using what we know we can set up an equation to solve for k, the number of stories in our pyramid.
47 = sigma(3n - 1, n, 1, k)
With our equation in it's current form there is no clear-cut way to solve for k, so let us review what we have before us:
Since this is just a sum we can factor out:
3*sigma(n) - sigma(1)
The last term here can be rewritten as a product:
3*sigma(n) - k*1
So we now have something more managable, but we still have a sum to to contend with.
sigma (n, n = 1, k), if you examine it, is a sum of an arithmetic sequence.
How so? An arithmetic sequence is a sequence of numbers all separated by a common difference.Hence, a list of numbers like 2,4,6,8... could be said to be an arithmetic sequence becaues all of its terms are separated by a common difference of 2.
In myPrecalculus class I learned a formula for the sum of n terms in an arithmetic sequence:
We can replace the sigma sum with this formula, and this will make solving our equation much easier.
After simplify we end up with a quadratic equation:
We got two roots, both of with turn out not be integers, so this led me to suspect that there were not 47 cards in that pyramid. After plugging different values of k into the formula I decided that there were 57 cards in it. (The next lower number was 40, which was too low)
Changing 47 to 57 in the quadratic equation yielded the roots 6 and -19/3. It is understood that there is no such thing as a pyramid with negative stories, so we can conclude that there were 6 stories in the pyramid! Hurrah!