Índice
 
RECONSTITUIÇÃO do sinal digital em analógico.
 
 
A reconstituição correta do sinal analógico, a partir do sinal digital, é feita em duas etapas :

1 -  Decodificação e conversão digital para analógico D/A dos bits em amostras PAM.
2 -  Filtragem do sinal PAM por um filtro passa baixo com freqüência de corte igual a freqüência de Nyquist (ou seja, metade da freqüência de amostragem).

A decodificação e conversão D/A é feita por um conversor digital-analógico DAC, que transforma cada grupo de n bits de em um pulso PAM com nível analógico igual ao valor quantizado.

A reconstituição explicada no domínio do tempo :

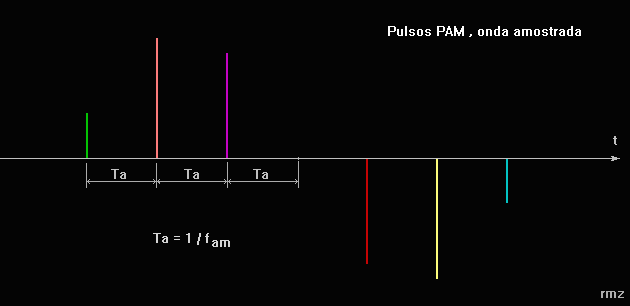
Como preencher os espaços vazios entre as amostras PAM ?  Ou seja, como completar corretamente a infinidade de pontos que estão faltando entra as amostras ?  Esta é a função do filtro passa baixo. A figura seguinte é um exmplo de sinal PAM a ser reconstituido em sinal analógico :

Resposta impulsional de um filtro passa baixo ideal.

Quando um filtro passa baixo ideal (com roll-off = zero) é excitado na sua entrada por um impulso, o sinal na sua saída tem a forma senx / x, como mostra a figura seguinte :

Características importantes na resposta impulsional de um filtro passa baixo ideal, com freqüência de corte fo :
- o impulso de entrada é um pulso de curta duração t tal que  t << 1 / 2fo.
- a amplitude do sinal de saída é proporcional a energia do pulso de entrada, portanto proporcional a amplitude do pulso, desde de que sua duração t seja fixa e dentro do critério acima.
- o sinal de saída tem forma sen x / x , portanto passa por zero em tempos múltiplos inteiros de T = 1 / 2 fo, exceto no ponto de máxima amplitude. O tempo T independe da duração t do pulso de entrada, desde que t << 1 / 2fo.

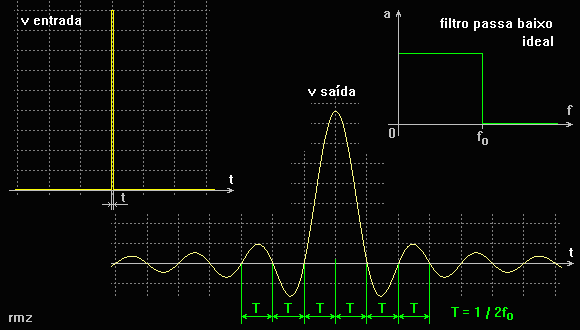
Se em vez de um único pulso, excitamos o filtro com uma seqüência de pulsos PAM, com cadencia exatamente igual a T = 1 / 2 fo, então estes pulsos não interferirão entre si, pois cada um cairá num ponto zero da resposta impulsional dos seus antecessores e/ou dos seus sucessores.
Se o intervalo entre os pulsos PAM não for exatamente T , teremos interferência no nível de qualquer pulso pelas respostas individuais dos pulsos anteriores ou posteriores, chamada interferência intersimbólica I I S.

Reconstituição do sinal analógico :

A freqüência fundamental dos pulsos PAM, que é a freqüência de amostragem deve ser igual ao dobro da banda passante fo do filtro passa baixo.
Portanto, o nível de saída do filtro, nos citados pontos de zero, será exatamente proporcional ao nível de cada um dos respectivos pulsos de entrada, não introduzindo nenhum erro nos níveis dos pulsos PAM. Nos intervalos entre os pontos zero da resposta sen x / x, o sinal de saída do filtro será o somatório de todos os níveis positivos e negativos das respostas impulsionais presentes neste intervalos, reconstituindo exatamente a forma de onda analógica original  que esta faltando entre as amostras. (a menos do erro de quantização que foi introduzido na geração do sinal digital, e que evidentemente não tem mais jeito de ser compensado, pois o seu valor é desconhecido).
Este é um dos famosos critérios que Nyquist estipulou em 1928, para transmissão de sinais digitais, e que se aplica também a reconstituição. No caso de reconstituição de sinal, já que a freqüência de amostragem foi definida na geração e não podemos mais altera-la, podemos concluir que a freqüência de corte do filtro passa baixo ideal deve ser exatamente igual a metade da freqüência de amostragem, para que os pulsos PAM possam ser transformados em uma onda analógica continua e sem interferência intersimbólica.

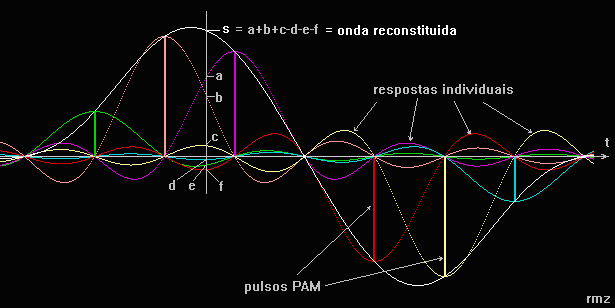
A figura seguinte mostra como um sinal PAM, de amostras descontinuas, é transformado no sinal analógico original, em branco. Em cores estão cada pulso PAM e a respectiva resposta impulsional do filtro, para cada pulso tomado individualmente, sem os outros. A curva branca é a resultante do somatório, a cada instante, das curvas coloridas.

 
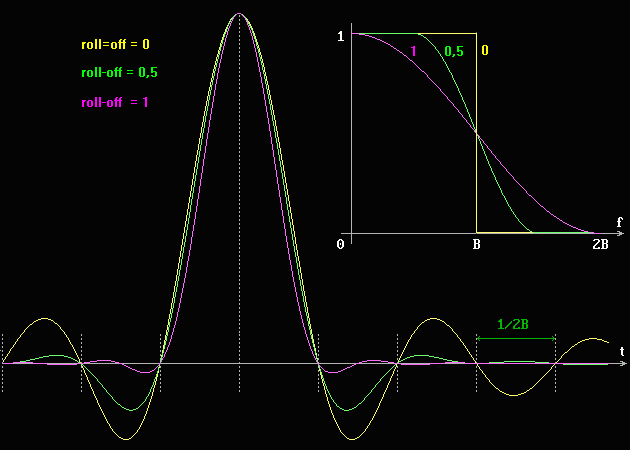
Na saída do filtro, temos a onda analógica continua original (com ruído de quantização) :
O que vimos acima depende de um filtro passa baixo ideal. Como esse filtro não existe na prática, qual é o filtro real que permite o mesmo resultado ?  Outra vez, Nyquist já tinha pensado nisso em 1928 !...quando deduziu outro dos famosos critérios, o da simetria vestigial, que diz o seguinte :

A adição de uma função de transferencia real e de inclinação simétrica em torno da freqüência de corte à função de transferencia do filtro passa baixo ideal, mantém os pontos de cruzamento do eixo zero da resposta impulsional. Estes pontos definem a condição necessária para transmissão livre de I I S.

Em outras palavras, se o filtro real tiver um roll-off  por exemplo em forma de coseno levantado, a sua resposta impulsional terá os zeros no mesmo lugar da curva sen x / x, mas o aspecto da curva será diferente. A figura seguinte mostra  um exemplo de filtro passa baixo com roll-off em forma de cosenoide levantada, que é a região onde o filtro passa gradativamente de passante (on) para o corte (off). Esta região é simétrica em relação ao ponto fo. 
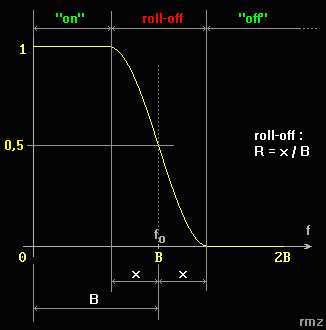
 Por definição,  o roll-off  R é igual a R = x / B  e pode variar de zero (filtro ideal) até 1 ou 100% quando x = B. Neste caso, o filtro só corta mesmo em f = 2fo = 2B. Similarmente, o roll-off também se aplica a fitros passa faixa.

 
A figura seguinte mostra as respostas do filtro passa baixo para roll-off de 0 ,  0,5  e 1 :
Detalhe : para roll-off = 1, existem zeros adicionais no meio dos zeros originais, que permanecem.
 
A reconstituição explicada no domínio da freqüência :

É sabido que o espectro dos pulsos PAM contem uma enorme quantidade de raias, desde a raia com freqüência zero (a componente contínua), e múltiplos inteiros da freqüência de amostragem : fam, 2fam, 3fam, ... Estas raias todas são moduladas em AM pelo sinal analógico quantizado, e consequentemente tem bandas laterais superiores e inferiores iguais a banda do sinal analógico quantizado. Portanto, a raia zero contem a banda lateral de zero até fam/2 = fn, que é exatamente a banda do sinal quantizado.

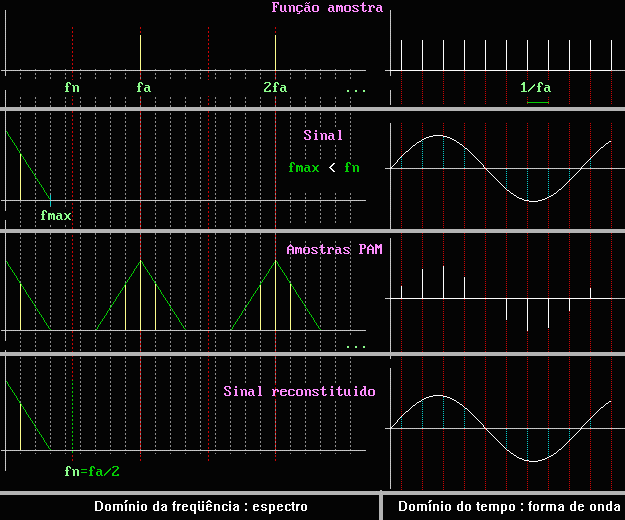
Basta então fazer passar o sinal PAM por um filtro passa baixo com freqüência de corte igual a freqüência de Nyquist = fam/2 para restituir o sinal analógico continuo.
Só não é possível mostrar porque o filtro real deve ter roll-off simétrico, como foi mostrado no domínio do tempo.

Obs.: o programa RZ2 permite fazer diversas demonstrações do que foi visto acima, com possibilidade de alterar varios parâmetros de forma interativa.

  Índice