IN3OTD's web site
...under perpetual construction.

Variometer Design
A variometer consists usually of two coaxial coils, connected in series, where the coils relative position can be varied in some way. If L1 and L2 are the self-inductances of the first and second coil and Lm is the mutual inductance between the two, the total inductance can be written as Ltot=L1+L2±2Lm. The mutual inductance is defined as the flux linked by the turns of an inductance when the other carries a unit current; this of course depends not only on the coil length and diameter but also on their relative position.
For two coaxial coils, like the ones in the picture, the mutual inductance is at maximum when they are also concentrical, i.e. D=0.
If the two concentrical coils are rotated, so that their axes are not parallel any more, the mutual inductance decreases, reaching zero (almost) when the angle is 90°. Continuing the rotation beyond 90° the mutual inductance increases again, but this time with the opposite sign. So, according to the above formula, rotating a coil 180° gives a variation of the total inductance of 4Lm.
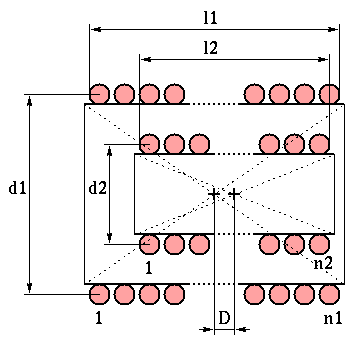 If the two coaxial coils are moved along their axis instead (D<>0), the mutual inductance decreases, eventually reaching zero at infinity, but does not change sign. This means that there is less variation in the total inductance just moving the coils with respect to rotating them.
If the two coaxial coils are moved along their axis instead (D<>0), the mutual inductance decreases, eventually reaching zero at infinity, but does not change sign. This means that there is less variation in the total inductance just moving the coils with respect to rotating them.
The form below computes the main parameters for the two types of variometer described above. The self-inductances are calculated using the formulas in [1], while the mutual inductances use the formulas from [2], with some minor corrections.
These formulas agree very well with the results of some electromagnetic simulations I have done, see the page for details.
References:
| [1] | R. Lundin, "A Handbook Formula for the Inductance of a Single-Layer Circular Coil," Proc. IEEE, vol. 73, no. 9, pp. 1428-1429, Sep. 1985. |
| [2] | F.E. Terman, "Radio Engineers' Handbook," London, McGraw-Hill, 1st ed., Sep. 1950. |